損失関数として使われる交差エントロピー誤差をpython3で表してみよう。

まず数式はこちら。

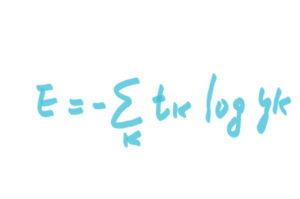
(ちなみに、画像はスマホのLINE BRUSHってやつで書いている。なので、ちょいと見づらいのはご愛嬌。)

tkは正解ラベル。
ykはニューラルネットワークの出力。

python3コードはこちら。

[py]

def entroErr(y,t):
    dlt=1e-8
    return -np.sum(t * np.log(y + dlt))

[/py]

では、実際に動かしてみる。

まず、yに値を入れる。
値は適当だが、左から３番目を一番大きい値に設定。
>>>y=[0.1,0.15,0.5,0.1,0.15]

お次はtの正解ラベルに値を入れる。
ちなみに、one-hot表現ってやつ。
この場合は左から３番目が正解。
>>>t=[0,0,1,0,0]

で、上記のpythonコードを試してみる。
pythonインタプリタで上記コードを入力。
インデントは要チェック。

>>> def entroErr(y,t):
… dlt=1e-8
… return -np.sum(t * np.log(y + dlt))

先ほどのy、tを引数にentroErr関数を試す。
>>> entroErr(np.array(y),np.array(t))
0.69314716055994541

これだけだと比較のしようがないので、yの値を変更してみる。

>>> y=[0.1,0.5,0.15,0.1,0.15]
>>> y
y=[0.1,0.5,0.15,0.1,0.15]

で、もう一度実行。
>>> entroErr(np.array(y),np.array(t))
1.8971199182192169

正解時の結果
0.69314716055994541

不正解時の結果
1.8971199182192169

てことは、正解時の方が損失関数の値が小さいので、
正しく動いているってことですね。

この損失関数の値をできるだけ小さくする（その時の重みパラメタを更新）のが、ディープラーニングの学習目標でもあるので、行数は短くても結構大事なコードってことですね。